Finding the discriminant

When finding the discriminant of a solution the equation is b^2 -4ac . You use this equation to find the number of solutions an equation has.  Lets say you have the equation x^2 +6x +9=0 . First you identify a,b & c . In this equation a=1 , b=6 & c=9 , you plug all the letters into the equation to get 6^2-4(1)(9)=0 which equals 0. When getting this final answer you have to know that if the answer is less than 0 there is no solution, when it is greater than 0 you will get 2 solution and if it equals 0 you will get 1 solution. Since the answer was 0 , the number of solutions is 1.

Solving Linear Systems that are quadratic

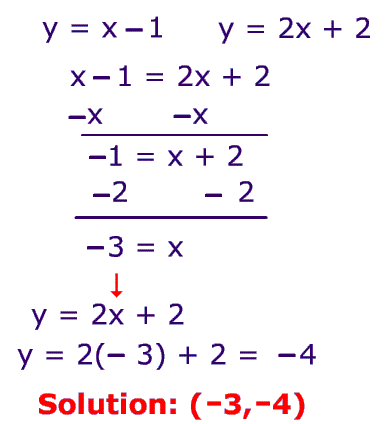
When solving linear systems , like the one above; you have to make both equations equal each other. Then you have to get ride of one x. After this you get ride the number that is with the x by using the opposite equation. (like shown above ). After you find x you have to plug it back in to one of the original equations in order to find the y.

Multiplying Rational expressions

 As You can see from the picture on your left, when you multiply rational expressions, you first have to factor out all the numerators and denominators so they can be in simplest form. After you have done this you can cross of any factors that can cancel out. For example , the (x+2)  on one fraction can cross of with the (x+2) on the other fraction; this is shown with the pink line over them. The next thing you can cross of is the (x-2) on one fraction and the (x-2) on the other fraction. The last thing you can cross of is the x on both fractions. This leaves you with x-1/x+2 as your final fraction.

solving rational proportions

When solving rational proportions you are trying to solve for x. In this proportion x + 3/4=2/5 you have to cross multiply and distribute. when this is done you should get this 5(x + 3) = (4)(2) then 5x + 15 = 8 in order to get x by its self you have to get ride of the 15. so you have to do the opposite operation and subtract 15 from both sides of the equal side. That becomes 5x = -7 you divide by 5 on both sides in order to get x alone. & your final answer would be x= -7/5

Adding & Subtracting more complex rational expressions

When adding or subtracting more complex rational expressions like unlike denominators , you have to find the least common denominator, then just add or subtract normally.


2y =2 * y
3y^2 = 3 * y * y
Use each prime factor the greatest number of times
it appears in each.
LCD: 2 * 3 * y * y or 6y^2

Change each rational expression into an equivalent
expression with the LCD by multiplying the top and bottom by the same numbers/variable like this:

5/2y + 4/3y^2 = 5(3y)/2y(3y) = 4(2)/3y^2(2) which becomes 15y/6y^2 + 8/6y^2   which equals 15y+8/6y^2.

adding and subtracting rational expressions

When adding or subtracting rational expression you always have to see that the denominators are the same. For example, when subtracting 6/5d and 2/3d you have to find a common denominator. To do this you can multiply each by each other. For example 5d and 3d have the same variable so you can leave that alone but you have to change the number, so you would multiply 5 times 3 to get a common denominator. So the common denominator would be 15d. But what ever you do to the bottom you have to do to the top. So the new expression would be 18/15d-10/15d. lastly you just subtract the numerators and leave the denominators alone. So your final answer would be 8/15d.

dividing rational expressions

When diving rational expressions, first thing you have to do is find the reciprocal of the second term. As shown in the example. Rewrite the expression to make things easier. Then look at the expressions and factor any that is not. After if there is any terms that can "cancel out" get rid of them as shown in the example. Rewrite the final answer and your done.

Dividing Polynomials

When factoring polynomials you have to make sure both the denominator and numerator are both factor out . For example, x^2+2x+1/ (x+1) , the numerator is not factored.After you factor you should have                         (x+1)(x+1)/(x+1). (x+1) / (x+1) becomes 1 and 1 times (x+1) equals x+1 as your final answer.

Factoring Trinomials

When factoring trinomials first make sure your equation is in simplest form. For example x^2+10x+25 , when this is done you have to figure out two numbers that add up to 10 and also multiply to 25. You can list all the common  factors until you find the correct one. For this problem 5 and 5 are the two numbers that add up to 10 and multiply to 25. After this you factor it, since there is x^2 those factor out to x and x the you just add the 5's and your answer will be (x+5)(x+5)

Multiplying Binomials

When multiplying you can use a method called "the box method"., this method is a simpler way  to use the distributive property. 

For Example: in this image we see (x+2)(x+3) . First you multiply 2 and x to equal 2x. Then 2 and 3 to make 6.  Then you multiply x and x to make (x)(x) which can also be said as x squared. After that you multiply x and 3 to make 3x. When your done with this step you end up with 2x+6+x^2+3x, combine like terms and your answer is x^2+5x+6.

Solving Diamond Problems

When solving diamond problems you have to find the numbers that are the product of the greater number and the sum of the smaller  number. For example:

As you can see the two numbers are 12 and 7. We have to find two numbers that when multiplying will equal 12 and when adding equal 7. You can list the factor of 12 to make it easier. Of those factors you have to see which one sums up to 7. 1 +12 and 2+6 does not equal 7 so the answer has to be 3 and 4. Now your finished.

Classifying Polynomials

When classifying polynomials you have to find the number of degrees and the number of terms and name them.

For Example- the polynomial 7x+4 has a degree of 1 and has 2 terms. So you would classify the degree as "linear" and the terms as "binomial".