Finding the discriminant

When finding the discriminant of a solution the equation is b^2 -4ac . You use this equation to find the number of solutions an equation has.  Lets say you have the equation x^2 +6x +9=0 . First you identify a,b & c . In this equation a=1 , b=6 & c=9 , you plug all the letters into the equation to get 6^2-4(1)(9)=0 which equals 0. When getting this final answer you have to know that if the answer is less than 0 there is no solution, when it is greater than 0 you will get 2 solution and if it equals 0 you will get 1 solution. Since the answer was 0 , the number of solutions is 1.

Solving Linear Systems that are quadratic

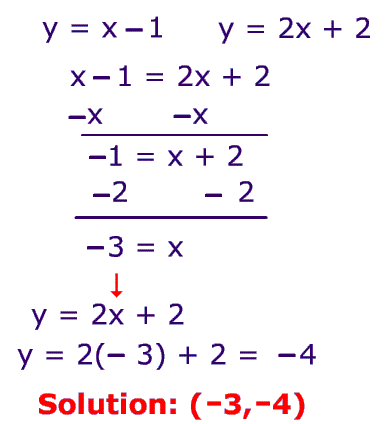
When solving linear systems , like the one above; you have to make both equations equal each other. Then you have to get ride of one x. After this you get ride the number that is with the x by using the opposite equation. (like shown above ). After you find x you have to plug it back in to one of the original equations in order to find the y.

Multiplying Rational expressions

 As You can see from the picture on your left, when you multiply rational expressions, you first have to factor out all the numerators and denominators so they can be in simplest form. After you have done this you can cross of any factors that can cancel out. For example , the (x+2)  on one fraction can cross of with the (x+2) on the other fraction; this is shown with the pink line over them. The next thing you can cross of is the (x-2) on one fraction and the (x-2) on the other fraction. The last thing you can cross of is the x on both fractions. This leaves you with x-1/x+2 as your final fraction.

solving rational proportions

When solving rational proportions you are trying to solve for x. In this proportion x + 3/4=2/5 you have to cross multiply and distribute. when this is done you should get this 5(x + 3) = (4)(2) then 5x + 15 = 8 in order to get x by its self you have to get ride of the 15. so you have to do the opposite operation and subtract 15 from both sides of the equal side. That becomes 5x = -7 you divide by 5 on both sides in order to get x alone. & your final answer would be x= -7/5

Adding & Subtracting more complex rational expressions

When adding or subtracting more complex rational expressions like unlike denominators , you have to find the least common denominator, then just add or subtract normally.


2y =2 * y
3y^2 = 3 * y * y
Use each prime factor the greatest number of times
it appears in each.
LCD: 2 * 3 * y * y or 6y^2

Change each rational expression into an equivalent
expression with the LCD by multiplying the top and bottom by the same numbers/variable like this:

5/2y + 4/3y^2 = 5(3y)/2y(3y) = 4(2)/3y^2(2) which becomes 15y/6y^2 + 8/6y^2   which equals 15y+8/6y^2.